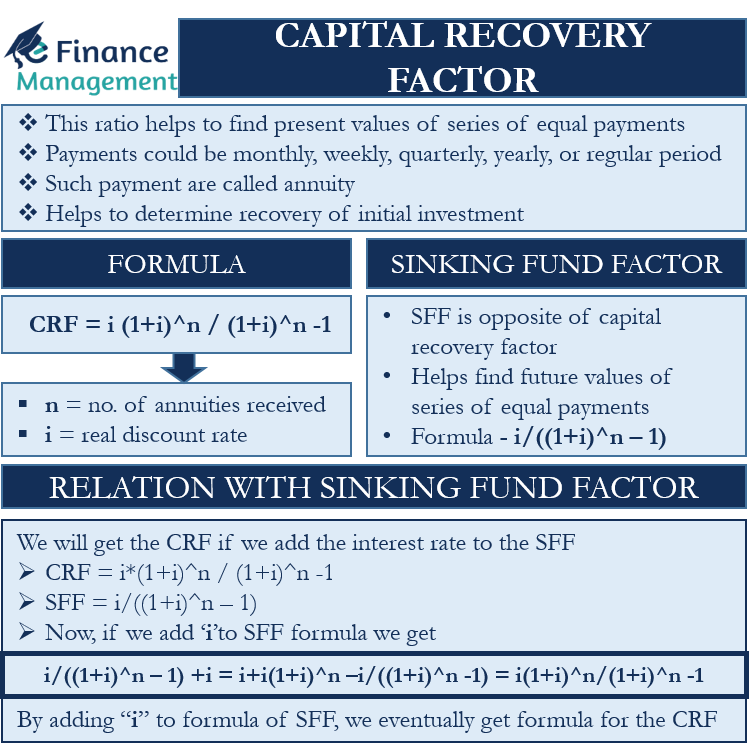
Capital Recovery Factor (or CRF) is the ratio that helps to find the present values of a series of equal payments. The equal payments could be monthly, weekly, quarterly, yearly, or any other regular period. We generally call such payments annuities. So, we can say that the capital recovery factor assists in finding the present values of the annuities.
The term capital recovery factor comes from the word capital recovery. Capital recovery means recovering the initial investment made. Thus, the CRF helps to determine the recovery of the initial investment.
Moreover, this factor is a valuable cost analysis tool. Start-ups and investors regularly use it to find the success of their investment.
Capital Recovery Factor – Formula
CRF converts the present value of series payments over a fixed amount of time. Thus, the formula for CRF is:
CRF = i (1+i)^n / (1+i)^n -1
Here “n” is the number of annuities received, and “i” is the real discount rate. The CRF formula is very similar to the annuity formula.
Let’s understand the concept of CRF with the help of an example.
Assume the real discount rate (i) to be 7% and the number of annuities received (n) 5 years. Using the formula, we get CRF equal to 0.2439.
Also Read: FVIF Calculator
Now assume a $1,000 loan at 7% interest needs to be paid back in five annual payments. So, the five annual payments will be $243.90 each. Using the CRF, we can say that the present value of the five annual payments of $243.90 is $1000.
Relation with Sinking Fund Factor
The Sinking Fund Factor is the opposite of the capital recovery factor. Like CRF helps determine the present values of a series of equal annual cash flows, the sinking fund factor helps find the future values of the series of equal payments.
The formula to calculate Sinking Fund Factor is:
i/((1+i)^n – 1)
Talking about the relation between the two, we will get the Capital Recovery Factor if we add the interest rate to the Sinking Fund Factor. Let’s see how:
Capital Recovery Factor = i*(1+i)^n / (1+i)^n -1
Sinking Fund Factor = i/((1+i)^n – 1)
Now, if we add “i” to Sinking Fund Factor formula we get:
i/((1+i)^n – 1) +i = i+i(1+i)^n –i/((1+i)^n -1) = i(1+i)^n/(1+i)^n -1.
So, by adding “i” to the formula of the Sinking Fund Factor, we eventually get the formula for the Capital Recovery Factor

