Weighted Average cost of capital (WACC) is the minimum rate of return required to create value for the firm. Investors of equity, debt, preference shares, etc., have sufficient reason to continue investing in the firm if it earns a return equal to or more than WACC. The formula for calculating WACC is simple. Like all the other concepts, WACC also has certain advantages and limitations.
Definition
It is the weighted average of the cost of equity, preferred debt, and any other capital. The weights used for averaging are the quanta of capital supplied by respective capital. For example, assume a firm with the cost of capital of debt and equity as 6% and 15% having an equal share in capital, i.e., 50:50, the weighted average cost of capital would be 10.5% (6*50% + 15*50%).
WACC is the minimum rate of return required to create value for the firm. Any project with a rate of return less than WACC will reduce the firm’s stock prices. This rate works as the hurdle rate for project evaluation, provided the new project is financed in the same fashion as the firm’s current mix of capital and the risk profile of new projects is similar to existing ones.
Refer: Importance and Use of Weighted Average Cost of Capital (WACC)
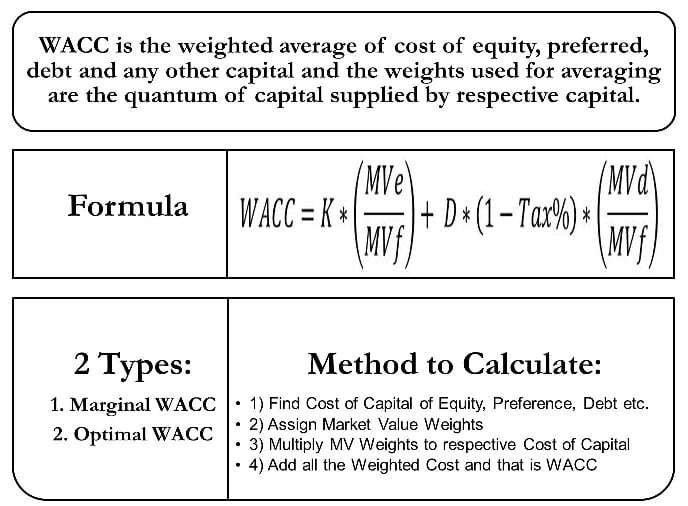
Method to Calculate WACC using Formula
The method for calculating the weighted average cost of capital is very simple.
- Determine the cost of capital of equity, preference, debt, and any other capital.
- Assign the Market Value Weights by finding out the percentage of the amount of investment made by each form of capital in the firm’s total capital. (Refer: Market Value vs. Book Value WACC).
- Multiply the weights to the respective cost of capital to find out the weighted cost.
- Add the weighted cost of all the forms of capital to determine the weighted average of capital.
Formula using only Debt and Equity
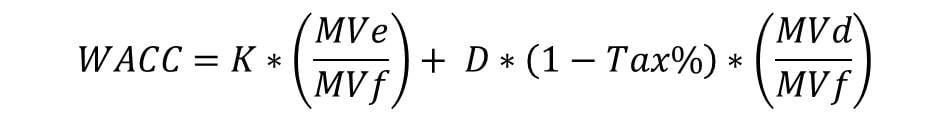
K = Cost of Equity Capital
D = Cost of Debt Capital
Tax% = Percentage of Tax
MVe = Market Value of Equity
MVd = Market Value of Debt
MVf = Market Value of Firm
Note: (1-Tax) is for applying the tax shield of debt and finding the actual cost of debt capital for the firm by eliminating the tax benefit received due to debt.
Also Read: WACC Calculator
Understand WACC with Examples
An example will serve the best understanding of calculations of WACC. Let us suppose a firm with the following capital mix. Equity, debentures, and preference shares are issued at the cost of capital of 20%, 8%, and 12%, respectively, with a total investment amount of $500, $200, and $250, respectively. The amount of capital consider is the market value of the capital.
The weights are calculated based on the amount of capital invested by each category of capital in comparison to the total capital, i.e., $950. The equity is 53% of total capital, the debenture is 21%, and the preference share capital is 26%. The weighted cost of each capital category is the multiplication of the cost of capital with respective weights.
| Type of Capital | Cost of Capital | Amt. of Capital | Weights | Weighted Cost |
|---|---|---|---|---|
| Equity Shares | 20% | $500 | 53% | 10.60% |
| Debentures | 8% | $200 | 21% | 1.68% |
| Preference Shares | 12% | $250 | 26% | 3.12% |
| Total | 950 | 15.40% (WACC) |
You can also use our WACC Calculator for calculations.
Types of WACC
Marginal Weighted Average Cost of Capital
Optimal Weighted Average Cost of Capital
Optimum WACC is the lowest cost of capital possible due to the optimum mix of capital. There are various theories for explaining the effect of the capital structure or mix on WACC. Such as Net Income Theory, Net Operating Income Theory, Traditional Theory, and Modigliani and Miller Approach.
Conditions / Assumptions for Use of WACC as Hurdle Rate
The use of WACC for evaluating the projects assumes some conditions. One, all the projects are undertaken by the company are of the same risk profile. Second, the source and mix of financing for the new projects is the same as the current capital mix of the company.
Also Read: How to Calculate WACC?
WACC as Hurdle Rate for Project Evaluation
The main advantage of using WACC for evaluating projects is its simplicity. The same rate can be used for all the projects, which will prevent all the individual project-wise different calculations.
The main limitation of using WACC is that it does not consider the floatation cost of raising the marginal capital for new projects. Another problem with WACC is its impractical assumption of the same capital mix, which is difficult to maintain.
RELATED POSTS
- Market vs. Book Value WACC
- Importance and Use of Weighted Average Cost of Capital (WACC)
- Advantages and Disadvantages of Weighted Average Cost of Capital (WACC)
- Project or Divisional Weighted Average Cost of Capital (WACC)
- Evaluating New Projects with Weighted Average Cost of Capital (WACC)
- Cost of Capital

