The present value of an annuity is a very interesting concept used by every one of us in day-to-day life. As the name suggests, it is about calculating the current value of the sum of cash flows derived from an annuity.
What is Annuity?
Annuity refers to the amount of money made in a series of payments made at regular intervals for a particular duration of time. For example, an investor receiving a sum of $1000 at the end of every year for a duration of 10 years is an annuity. Real-life examples of annuities are pension funds, bonds, or EMIs (Equated Monthly Installments). Pension funds promise the investor a fixed amount of income every year until their lifetime. Bonds pay regular fixed coupons (interest) at the end of every year until their maturity.
There are several types of annuity. The two main ones are regular annuity – where payments occur at the end of each period, annuity due – where payments are realized at the beginning of each period.
Purpose and Usage
The main motive behind calculating the present value of annuity payments is the concept of ‘time value of money.’
Time Value of Money
This concept explains the fact that a dollar in hand today is worth more than a dollar tomorrow because we can always invest the money we have in hand to get better returns for tomorrow. Also, taking the inflation factor into consideration, a dollar today will fetch more goods than a dollar tomorrow. In other terms, the purchasing power of a dollar decreases in due time if there is an inflationary environment in the economy.
Also Read: Ordinary Annuity vs Annuity Due
Situation 1
Let us examine a situation where two investment options are available for an investor, Investment 1 and Investment 2. Investment 1 guarantees the investor $1000 at the end of each year for a duration of 10 years. Investment 2 promises him a lump sum of $10,000 in the first year. Which one should the investor choose?
This is where the concept of calculating the present value of future cash flows comes into the picture.
How to Calculate the Present Value of an Annuity
An annuity is the collection of cash flows occurring at the end of each period (regular annuities). The present value of the total cash flows of an annuity is calculated by adding up the present values of each cash flow of all the years. The present value of any future cash flow is calculated by discounting it with a ‘discount factor’ or the required rate of return.
For calculation, you can use PVIFA Calculator
Formula of PVA
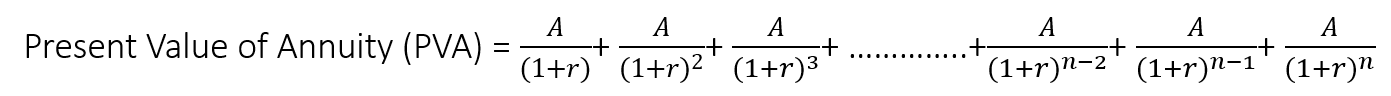
OR
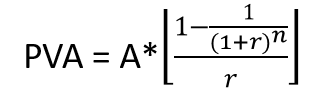
A = the constant amount of cash flows received every year
r= required rate of return
n= duration of the annuity
Example 1: Calculate the present value of a 5-year annuity of $10,000. The discount rate is 10%
Solution:
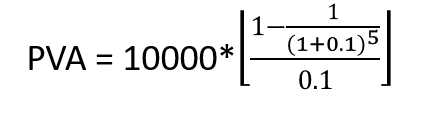
= $37,907
Now coming back to situation 1, let us examine which investment option is better for the investor, given the discount factor is 10%
Investment 1:
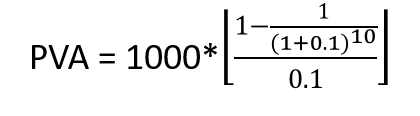
= $6,144.5
Investment 2: $10,000
Hence, the second investment option yields a return of $3,855.4 more than the first investment option. Hence, the investor should choose to opt for a lump sum payment of $10,000 in the first year itself.
Situation 2:
Few hybrid securities combine insurance and investment options. They usually collect a premium from the investor for a certain duration. They then promise him to pay part of the returns (the rest of the part goes to insurance) in annuity after the completion of a particular period. In this situation, how to calculate the present value of an annuity that starts after a certain duration (or does not start immediately)?
Also Read: PVIFA Calculator
Example 2: An Investor receives an amount of $1000 every year for a duration of 10 years. This will happen for 8 years now. Calculate the present value of this annuity if the required rate of return is 8%
Solution:
Step 1: Calculate the current value of the annuity, assuming we would start receiving payments by the end of this year (i.e., year 7).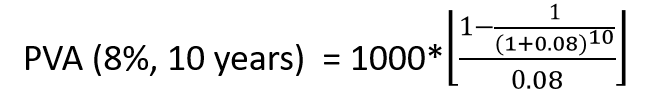
= $6,710
Step 2: Calculate the present value (PV) of the result in step 1 if the period is 7 years (i.e., current year).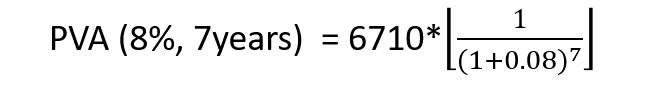
= $3,915.2
Hence, the present value of a $1000 value 10-year annuity at an 8% interest rate after 8 years is $3,915.2.
Read more at Annuity Formula
Relationship with Interest Rate Environment
The present value of annuity changes as the interest rate environment in the economy changes.
From example 1, let us calculate the present value of the same annuity with a discount factor of 6%
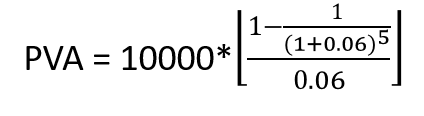
= $42,124
The PVA calculated at a lower discount rate (6%) is higher than the PVA calculated at a higher discount rate (10%).
Hence, the higher the discount rate, the lower the present value of the annuity.
Read more about Ordinary Annuity vs. Annuity Due – All You Need to Know.

