Total Factor Productivity

What is Total Factor Productivity?

Total factor productivity is a measure of efficiency and extent of the utilization of inputs in a production process. Also commonly known as TFP, it is the portion of output that does not has an explanation for a corresponding number of inputs (materials and labor) that we use in the production process. To put it simply, it is the ratio of output to the aggregate of inputs used for production. Or we can say it is the extra production/output than the identifiable inputs (material and labor) due to the contribution of other factors.

TFP is a good judge of operational efficiency in an organization. It tells us whether a business is channelizing its investments in the right direction or not. An increase in production capacity without a higher or at least a similar increase in production means improper utilization of business resources. It will directly affect the profits of the business, and hence, it needs to be taken care of right from the planning stage.

How to Calculate Total Factor Productivity?

The following are the two methods for calculating TFP.

Solow Residual

We can measure TFP growth by using the Solow residual. Robert Solow suggested this method in the year 1957. It is a measure of the number of goods or services that a business produces corresponding to all the inputs that we use to achieve that production. We use a weighted geometric average of the inputs that we use.

We divide the growth rate of the total output in an economy into two parts: the first part is the growth in the total output due to an increase in capital and labor, while we cannot account for the second part. This part denotes the growth that we get by changes in factor utilization, such as technological changes. So effectively, the Solow residual represents the gap or the difference in the growth rate of production vis-a-vis the incremental usage of the inputs. 

Assumptions

We make the following assumptions while using the Solow residual:

• The production function is neoclassical, i.e., the production function is linear and homogeneous,
• There is an accurate measurement of the growth rates of the inputs,
• Factor markets have perfect competition,
• We have constant returns to scale, i.e., capital share + labor share = 1,
• We can break down the growth of output distinctly between the growth of the factors of production and technical changes,
• We have a long-run time into consideration.

Equation

The equation for Solow residual is:

Solow residual = Gy – C * Gk – (1- C)* Gl

The equation of Solow residual comprises the following constituents:

Gy = Growth rate of aggregate output.

Gk = Growth rate of aggregate capital

Gl = Growth rate of aggregate labor

C = Capital share

In simple words, Solow residual is the difference between the rate of growth in aggregate production and the growth rate of physical capital and labor inputs. According to Robert Solow, out of the average growth rate of output per head achieved by the United States over the period 1940-49, only 12.5% was due to an increase in capital per worker, while the rest 87.5% was due to technological changes.

Example

Let us take one example to understand the above equation. Suppose the economy of the United States grows at a rate of 5% over a year. We further assume that Capital and Labor are the only available two factors of production The stock of capital grows at 7% per annum over the same period, while the labor force grows by 3% per annum. And suppose The share of capital in the total output is 1/3^rd or 0.33, whereas the share of the labor force is 2/3^rd or 0.66.

Therefore, we can calculate the TFP or Solow residual by substituting the values in our above formula.

TFP = 0.05 – {(0.33*.07) + [(1-0.33)*.03]}

= 0.05 – 0.0231 – 0.0198 = 0.0071

Hence, there is 0.7% of growth out of the total growth of 5% over the year that we cannot account for. This remainder is the Total Factor Productivity or the Solow residual. It is the measure of the technological progress over time that contributed to the growth of the total output.

Cobb-Douglas Equation

Paul Douglas and Charles Cobb gave us the Cobb-Douglas production function in the year 1927. This is another way to calculate the total factor productivity.

Equation

The Cobb-Douglas equation for total factor productivity is:

Y = A x Ka x Lb

Where, Y = Total product

A = Total factor productivity

K = Available capital

a = Output elasticity of capital

L = Available labor

b = Output elasticity of labor

Output elasticity of capital denotes the percentage change in total output due to a change in the capital as an input. Similarly, the output elasticity of labor is the percentage change in total output due to a change in labor as an input. They are usually lesser than one because of inefficiencies that exist with capital and labor.  

Any change in the available capital (K) or labor (L) will result in a change in total product (Y). In other words, we can calculate the total factor productivity by using this formula if we have the values of the rest of the variables.

We have other models also available for the calculation of the total factor productivity, suggested and provided by other prominent economists. Few of them are “Denison’s sources of growth,” and “Jorgenson- Griliches sources of growth” are two other prominent such models.

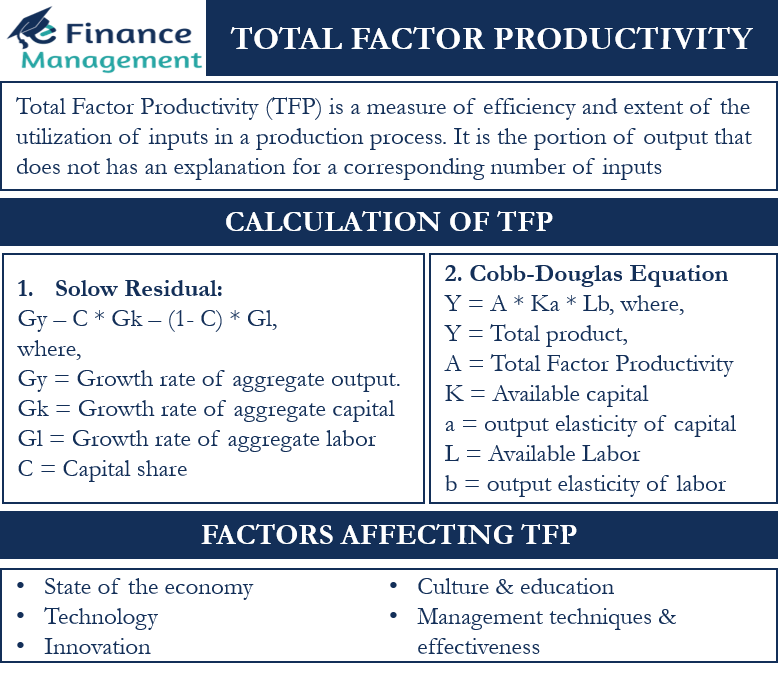
Factors affecting Total Factor Productivity

Let us learn what are the factors that affect total factor productivity.

State of the Economy

The factors have a relationship with the current economic status of the country/state, and that directly affects the TFP. Factors such as recessionary trends, high input costs, changes in demand, etc. have a direct impact on productivity. The fall in productivity will affect the TFP as well.

Technology

State-of-the-art technology, machinery, and production processes can help us to achieve high levels of efficiency in the production processes. We can derive a much higher output with the same level of capital and labor employed than what we were producing without implementing the new technology. This will help us to achieve higher TFP.  

Innovation

Innovation and constant research and development help us to find better ways of producing the same product or service. Hence, it also boosts production and, in turn, TFP.

Culture and Education

The culture in society can and does have a direct impact on productivity. An easy-going, laid-back attitude can result in lower productivity and TFP.

Education levels in society also affect TFP. Any economy with a highly educated and skilled workforce is bound to achieve high productivity levels with the same amount of capital and labor employed. Hence, we will have a high TFP in such economies.

Management Techniques and Effectiveness

Good management techniques such as proper allocation of work, effective control mechanisms, grievance redressal measures, etc. can help to boost employee trust and confidence in the management and the organization as a whole. Seamless undisturbed working with positive sentiments will definitely lead to improved productivity levels and TFP. 

Summary

Total factor productivity is an important barometer for ascertaining the efficiency of our production processes. In today’s world of cut-throat competition, businesses are looking for ways to deliver higher outputs with every corresponding input in their production processes. Total factor productivity helps to measure exactly how efficient and cost-effective their systems are. It also highlights and triggers the areas where the management can improve and beat the competition in the pursuit of staying ahead of their counterparts by changing their strategy and inputs.